Today I'm going to discuss cross-entropy and Binary cross-entropy. Before that, we need to understand the basics of the Sigmoid and Softmax function. Let's dive in.
Sigmoid Function
It squashes a vector in the range (0, 1). It is applied independently to each element and also called the logistic function.
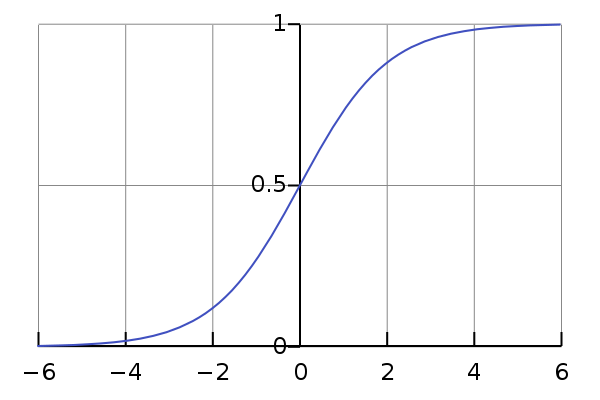
Formula of Sigmoid Function $$ f(x)={\frac {1}{1+e^{-x}}} $$
Let's understand by solving it...
Suppose you train the neural network and you get value x1 =1, x2 =9, x3 =424.5 , x4 = -3 , x5 = - 243
For x1 = 1, $$ f(x)={\frac {1}{1+e^{-1}}} = 0.731 $$ For x2 = 9, $$ f(x)={\frac {1}{1+e^{-9}}} = 0.999 $$ For x3 = 424.5, $$ f(x)={\frac {1}{1+e^{-424.5}}} = 1 $$ For x4 = -3 $$ f(x)={\frac {1}{1+e^{-(-3)}}} = 0.047 $$ For x5 = -243, $$ f(x)={\frac {1}{1+e^{-(-226)}}} = 2.99×10^{-98} $$
So what we are observed here is, the value of x tending towards positive infinity(∞), the sigmoid function converges to 1, and towards negative infinity(-∞), the function approaches to 0. The useful properties of the sigmoid function, as it tends towards a limit but always has a nonzero gradient.
Softmax Function
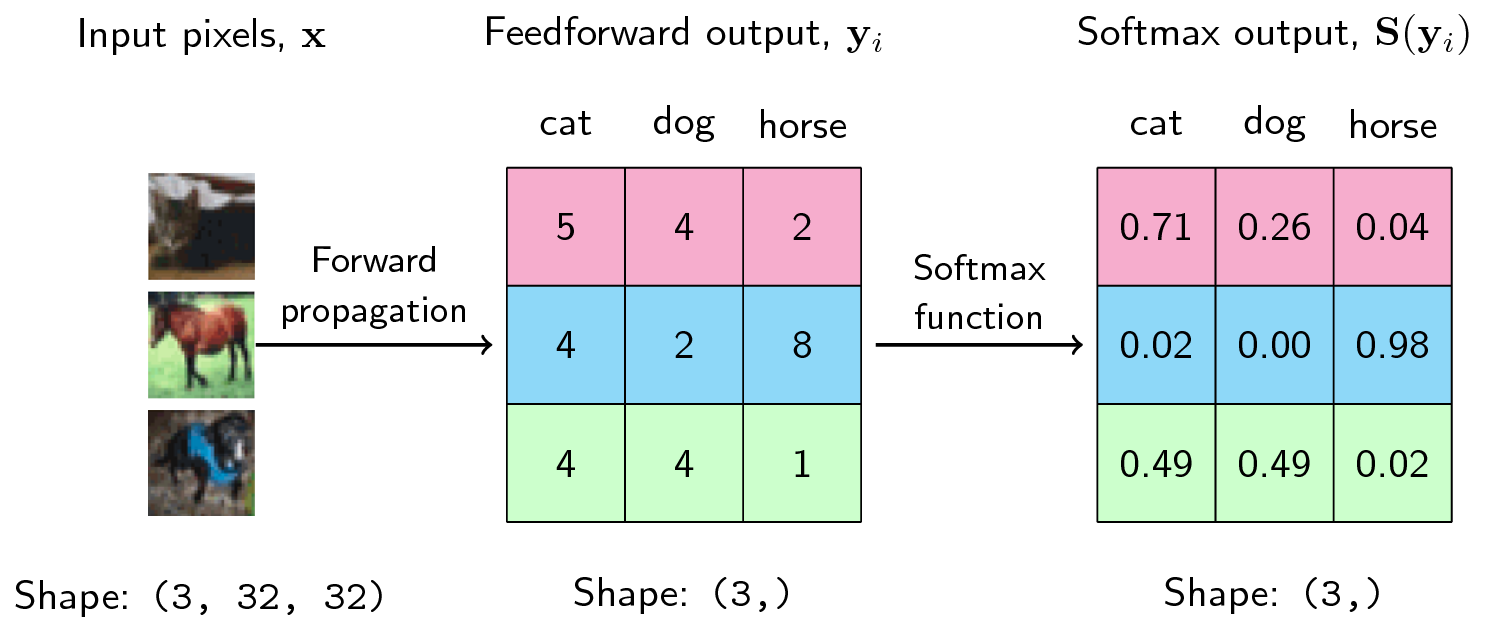
The softmax function takes as input a vector z of K real numbers and normalizes it into a probability distribution. The function turns real values that sum to 1. The input values can be positive, negative, zero, or greater than one, but the softmax transforms them into values between 0 and 1 so that they can be interpreted as probabilities. If one of the inputs is small or negative, the softmax turns it into a small probability, and if the input is large, then it turns it into a large probability, but it will always remain between 0 and 1.
Here is an example
The softmax formula is as follows:
Let's Calculating the Softmax
Suppose we have an output with these values and we want to convert the values into a probability distribution.
| Output (Z) | Value |
| Z1 | 3 |
| Z2 | 0.6 |
| Z3 | 6.3 |
See the calculation ->
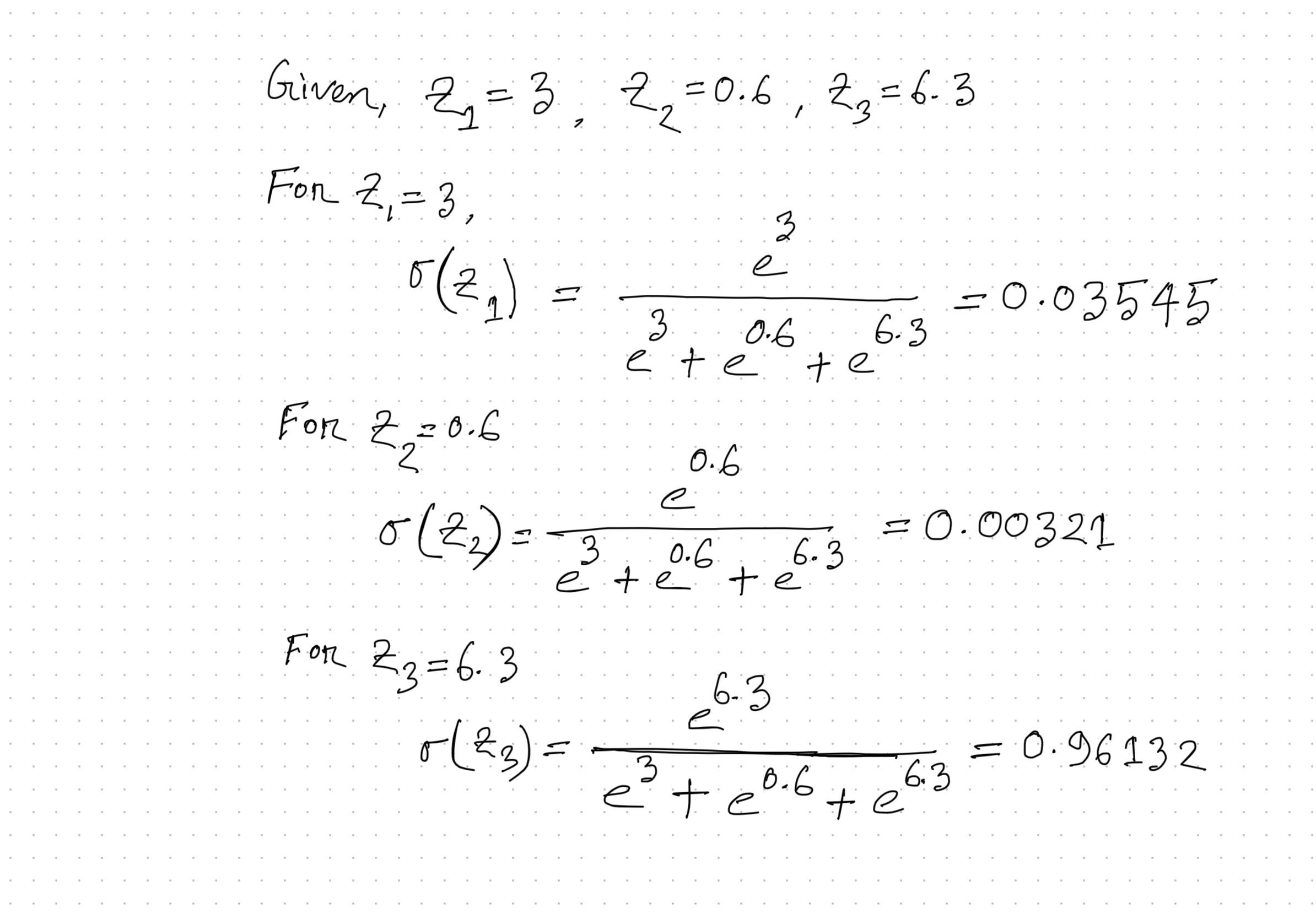
The higher score has a higher probability using softmax. Remember sigmoid function squash your score between 0 & 1 and on the other hand softmax function convert them into probabilities.
Neural Network
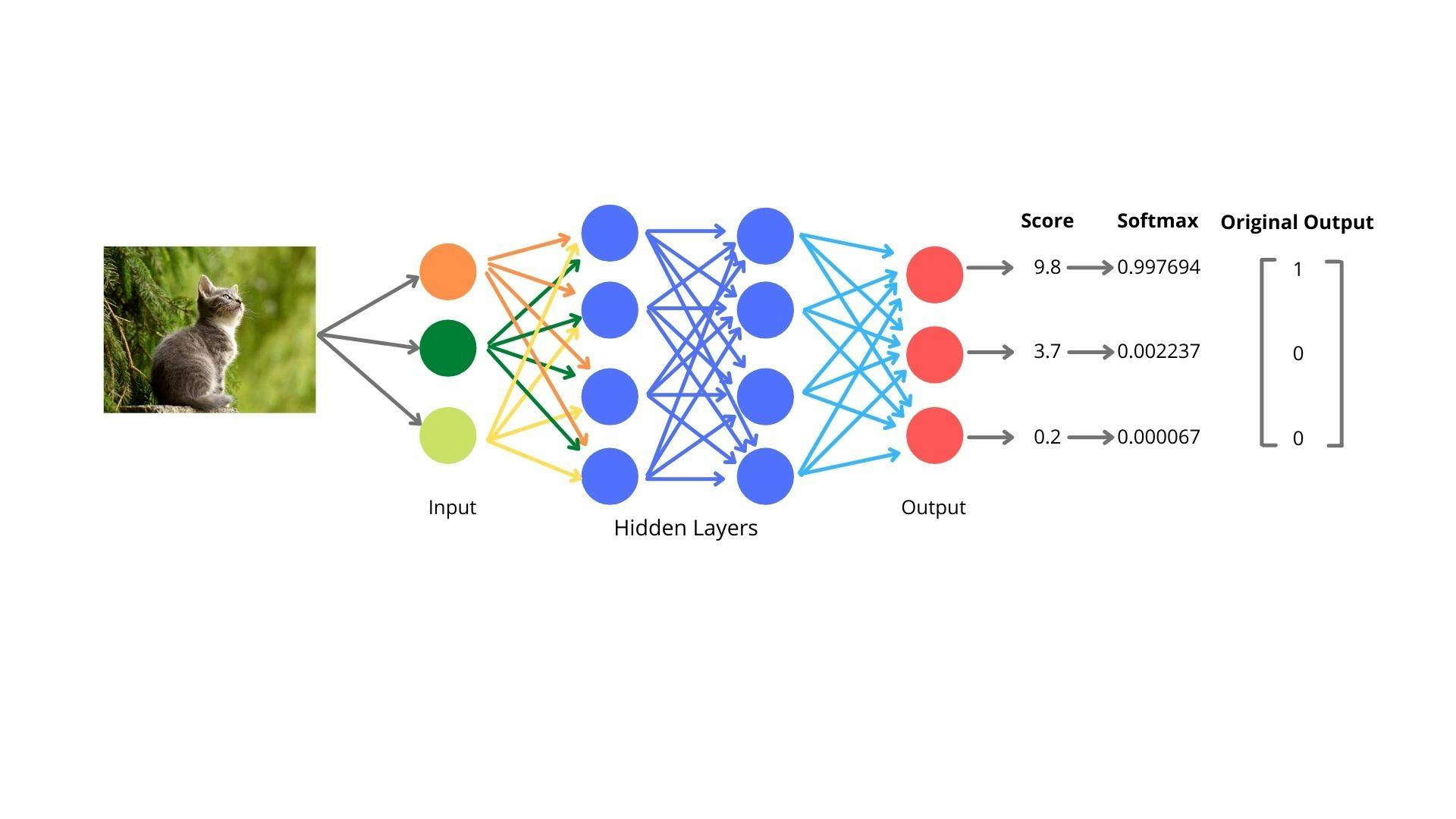
Imagine we have a convolutional neural network that is learning to distinguish between three classes which are cats, dogs, and birds. We set cat to be class 1 and dog to be class 2 and bird to be class 3.
Ideally, when we input an image of a cat into our network, the network would output the vector [1, 0,0]. When we input a dog image, we want an output [0, 1, 0]. When we input a bird image, we want an output [0, 0, 1]. This method called one-hot encoding. For every different class, make an encoding vector.
$$ Cat = \left[ \begin{array}{cc|c} 1\\ 0\\ 0 \end{array} \right] $$ $$ Dog = \left[ \begin{array}{cc|c} 0\\ 1\\ 0 \end{array} \right] $$ $$ Bird = \left[ \begin{array}{cc|c} 0\\ 0\\ 1 \end{array} \right] $$
Now we feed an image. The image pass through a couple of convolution layers. This final layer outputs three scores for cat, dog, and bird, which are not probabilities. Lastly, add a softmax layer to the end of the neural network, which converts the output into a probability distribution. So the cat image goes through and is converted by the image processing stages to scores [9.8, 3.7, 0.2]. Passing [9.8, 3.7, 0.2] into the softmax function we can get the initial probabilities [0.997694, 0.002237, 0.000067].
Cross-Entropy
The cross-entropy between two probability distributions p and q over the same underlying set of events measures the average number of bits needed to identify an event.
The cross-entropy formula \begin{aligned} H(p,q) &= - \sum\limits_{x \in X} p(x) \log q(x) \end{aligned}
$$ ProbabilityScore= \left[ \begin{array}{cc|c} q1 = 0.997694\\ q2 = 0.002237\\ q3 = 0.000067 \end{array} \right] $$
$$ OriginalScore = \left[ \begin{array}{cc|c} p1 = 1\\ p2 = 0\\ p3 = 0 \end{array} \right] $$
Now let's calculate, where p(x) is the Original Score and q(x) is Probability Score
For p1= 1 & q1= 0.997694 \begin{aligned} H(p1,q1) &= - 1 * \log_2 (0.997694) = 0.00333 \end{aligned}
For p2= 0 & q2= 0.002237 \begin{aligned} H(p2,q2) &= - 0 * \log_2 (0.002237) = 0 \end{aligned}
For p3= 0 & q3= 0.000067 \begin{aligned} H(p3,q3) &= - 0 * \log_2 (0.000067) = 0 \end{aligned}
As you can see, we multiple our encoded value with the probability score we get only one loss for one class. That means we correctly train our model to classify. So, this loss function is known as Categorical Cross-Entropy loss.
Binary Cross-Entropy
As we know for binary classification we need only C=2 classes. One class has label 1 and another one is 0.
Here is the formula for binary cross-entropy $$ loss = -{(y\log(p) + (1 - y)\log(1 - p))} $$
For binary, we need to classify one of 2 classes. So Let's classify cats vs dogs.
$$ Cat = \left[ \begin{array}{cc|c} 1\\ 0 \end{array} \right] $$
$$ Dog = \left[ \begin{array}{cc|c} 0\\ 1 \end{array} \right] $$
Let' Calculate binary cross-entropy where p = probability score and y = Original score
$$ ProbabilityScore= \left[ \begin{array}{cc|c} p1 = 0.997694\\ p2 = 0.002237 \end{array} \right] $$
$$ OriginalScore = \left[ \begin{array}{cc|c} Y = 1\\ Y = 0\\ \end{array} \right] $$
When classifying Cat, the probability score is p1 = 0.997694 $$ = -{(y\log_2(p) + (1 - y)\log_2(1 - p))}
= -{(1*\log_2(0.997694) + (1 - 1)\log_2(1 - 0.997694))} = 0.0033 $$When classifying Dog, the probability score is p2 = 0.002237 $$ = -{(y\log_2(p) + (1 - y)\log_2(1 - p))}
= -{(0*\log_2(0.002237) + (1 - 0)\log_2(1 - 0.002237))} = 0.0032 $$
As we can see from binary cross-entropy when our class is 1 the second part of the equation becomes 0 and when our class is 0 the first part of the equation becomes 0 .
This is the mathematical derivation of softmax, sigmoid, and cross-entropy.
Resources:
DeepAI: What is the Sigmoid Function?
Softmax Function
DeepAI:What is Softmax
Blog